In the olden days (sometime around the 5th century BCE), it was commonly believed that all numbers were rational and could be expressed as fractions with integer numerators and denominators. When Hippasus of Metapontum demonstrated that the square root of 2 is irrational, it challenged the Pythagorean worldview. According to legend, this revelation so outraged the followers of Pythagoras that they killed him for exposing a truth that contradicted their beliefs.
Throughout history, there have been numerous examples of groundbreaking discoveries causing outrage. Nowadays people (usually) don’t kill each other over disagreements or differences in ideology. However, there are still widely held beliefs that are not entirely correct or are oversimplifications of more complex phenomena.
We may have been wrong about statistical significancestatistically significant a result in statistical testing that provides enough evidence to reject the null hypothesis, suggesting that an observed effect is likely not due to chance alone all these years.
The NHSTNHST Abbreviation of null hypothesis significance testing paradigm in statistics
When I was in 10th grade and took statistics, I learned about the null hypothesisnull hypothesis a statement in statistical testing that posits no significant difference or relationship between variables, serving as the baseline assumption until evidence suggests otherwise. significance testing (NHST) paradigm. This framework plays a crucial role in scientific research and analysis. It’s widely used by researchers in biomedical and social sciences to evaluate their findings and draw conclusions from data. Additionally, it is a crucial part of the AP Statistics curriculum.
Null hypothesis (NH)
In NHST, the first step is to define a null hypothesis and an alternative hypothesis. The null hypothesis assumes that “nothing happens,” while the alternative hypothesis posits that our specific hypothesis is true and that “something happens.” For example, if we want to determine whether a coin is unfair (landing on heads more often), the null hypothesis would be that the coin is fair (50/50 odds of heads and tails), and the alternative hypothesis would be that the coin is unfair (>50% chance of heads).
The next step is to conduct the experiment or collect data. In the coin example, we would flip the coin some large number of times.
Significance testing (ST)
Imagine we flip the coin 10 times and get 9 heads. Is this just luck, or is the coin unfair? If we got 6 heads, it wouldn’t be surprising—that’s close to what we expect from a fair coin. But 9 heads seems unusual. To figure out if this result is meaningful, we use a method called significance testing . We calculate the chance of getting 9 or more heads out of 10 flips under the assumption that the coin is actually fair. This chance is called the p-value, and it tells us how surprising our result is.
Using the binomial distribution, we find that the p-value for 9 heads out of 10 flips is about 1% (or 0.01). This means if the coin were fair, we’d only expect to see this result (or something even more extreme) about 1% of the time. Researchers often use 5% (0.05) as a cutoff for significance. If the p-value is less than 5%, they call the result “statistically significantstatistically significant a result in statistical testing that provides enough evidence to reject the null hypothesis, suggesting that an observed effect is likely not due to chance alone” and reject the null hypothesis. If it’s more than 5%, they’re not able to reject the null hypothesis. In our case, 1% is less than 5%, so we’d say this result is statistically significant. We reject the null hypothesis that the coin is fair, which suggests our coin might not be fair after all.
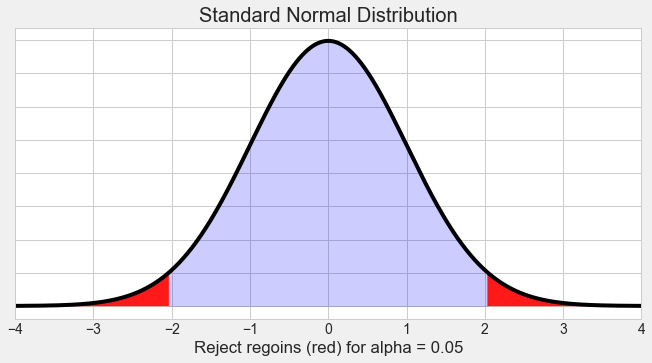
Credit: Smahdavi4 from Wikipedia
The standard statistical significance framework has problems
One thing I always found strange about this framework is that significance is binary. Results with a slightly higher than 5% chance of happening are considered nonsignificantnonsignificant a result in statistical testing that does not provide enough evidence (often a p-value < 0.05) to reject the null hypothesis, suggesting that any observed effect may be due to chance, viewed as no different from those that could occur by chance. On the other hand, results just below the threshold are considered evidence of a difference. However, I wanted to get a good score on AP Statistics, so I went along with it. I’ve recently found that others have found issues with this dichotomousdichotomous Something that has two possible outcomes or categories, often used in statistics or research to describe variables that can only be classified into two distinct groups. nature, validating my concerns [1]. These researchers suggest that the study should be evaluated based on its methodology and the significance on a continuum, not based on whether the significance crosses a specific threshold.
Another issue with the framework is the “replication crisis” in science. Unfortunately, many scientific journals are hesitant to publish nonsignificant results, fearing they would be viewed as uninteresting by their readership. However, even with absolutely no effect, there is a 5% chance of obtaining a significant result by chance. Additionally, researchers can inadvertently or deliberately increase their chances of finding a significant result. For example, they can selectively remove certain subgroups from their analysis until they achieve statistical significance. This phenomenon, known as “p-hacking,” can lead to the publication of studies that appear to show significant effects when, in reality, no true effect exists. Consequently, when other scientists attempt to replicate these results, they often fail to find the reported effect. It’s been estimated that more than half of psychology studies are unreproducible [2].
I find mostly nonsignificant effects
Lately, I’ve become interested in statistical significance and whether it is truly a good measurement. Many of the effects I’ve tried to estimate for Touche Stats ended up being nonsignificant. Nonsignificant results are often dismissed because researchers typically have small sample sizes, lacking enough “powerpower the probability that a study will correctly reject the null hypothesis when it is false, indicating the sensitivity of a test to detect an effect if it truly exists ” to detect an effect. The power is defined as the probability of rejecting the null hypothesis, given that there truly is an effect, and increases with sample sizesample size the number of individual observations or data points collected from a population for use in statistical analysis or experimentation. Insufficient power means there may be an effect, but the sample size is too small to distinguish it from chance. However, with my sample sizes of thousands of bouts, I always felt I had adequate power. What if there really is no effect?
Statistical nonsignificancenonsignificant a result in statistical testing that does not provide enough evidence (often a p-value < 0.05) to reject the null hypothesis, suggesting that any observed effect may be due to chance can be more informative than significance in economics
Statistical Nonsignificance in Empirical Economics
I’ve enjoyed reading much of Alberto Abadie’s work, such as his research on the synthetic control method. When I found out that he wrote a paper on nonsignificance [3], my interest was piqued. In this paper, he argues that nonsignificant results can be more interesting than significant ones in economics. This is because economists often work with large sample sizes, sometimes involving census data from thousands or millions of individuals. Abadie suggests that it is unreasonable to “put substantial prior probability on a point null,” meaning that assuming a “null hypothesis” in economics is often unrealistic.
Common effects that economists measure include the impact of changing minimum wage or early schooling on future performance. These interventions are likely to have some effect, even if it is very small. Therefore, researchers frequently achieve significance since the probability of rejecting the null hypothesis becomes very high with large sample sizes, even for a small effect. In this context, statistical nonsignificance becomes rarer than significance, signaling that there might be something particularly noteworthy to investigate.
Statistical Significance, p-Values, and the Reporting of Uncertainty
I also read a similar paper [4] written by Guido Imbens, whose work I also enjoy reading. He agrees with Abadie that it often does not make sense to assume the “null hypothesis” in economics. He also emphasizes the importance of assessing the “point estimatepoint estimate A single number calculated from sample data to estimate an unknown population parameter, like a mean or proportion ” (effect) of an interventionintervention a deliberate action or strategy implemented to produce a desired change or effect in a specific situation or system, not just its significance. If a result is significant but the effect is very small, like early schooling helping students answer just one extra question on a test with 1,000 questions, it’s not very impactful. Therefore, it’s more meaningful to evaluate the strength of the effect and its variability by constructing a confidence intervalconfidence interval a range of values calculated from sample data that is likely to contain the true population parameter, providing a measure of the uncertainty or precision of an estimate, which indicates where the effect is likely to fall 95% of the time. Then economists can decide whether the costs are worth the benefits.
Imbens also points out that the 5% threshold is arbitrary and mainly used to facilitate scientific communication. This standardized threshold fails to account for the significant variations across different research contexts. Researchers work with datasets and experimental setups of vastly different sizes and complexities, meaning false positives may be more common in some fields than others. The costs of these errors can also vary greatly depending on the field and the potential real-world implications of the research. Additionally, the plausibility of the null hypothesis can differ greatly across disciplines and specific research questions. Therefore, it doesn’t make much sense to use a one-size-fits-all approach to statistical significance.
Another issue he discusses is the tendency for results to be accepted simply because they are statistically significant, even when their findings appear bogus. For example, one study found that hurricanes with female names (e.g. Hurricane Katrina) cause statistically significantly more damage than hurricanes with male names. This study likely gained attention and publication primarily due to its statistically significant result, despite its questionable premise. He emphasizes the importance of vigilance against researchers who manipulate their models by testing multiple specifications and engaging in “p-hacking.”
Type M and Type S errors
Another thing I learned in statistics at school, are Type I and Type II errors. These are also part of the AP Statistics exam.
- Type I error: a false positivefalse positive when a statistical test incorrectly indicates that a condition or effect is present, when in reality it is not, where the null hypothesis is rejected even when there is no effect.
- Type II error: a false negativefalse negative when a test incorrectly indicates that a condition or effect is not present, when in reality it is, where the null hypothesis is not rejected even when there is an effect.
I recently discovered that another statistician who I like to read, Andrew Gelman, developed two new types of errors: the Type S and Type M errors [5].
- Type S (sign) error: when the test statistic (mean effect size found) is the opposite of the true effect size, given that the statistic is significant.
- Type M (magnitude) error: when the test statistic exaggerates the true effect size, given that the statistic is significant.
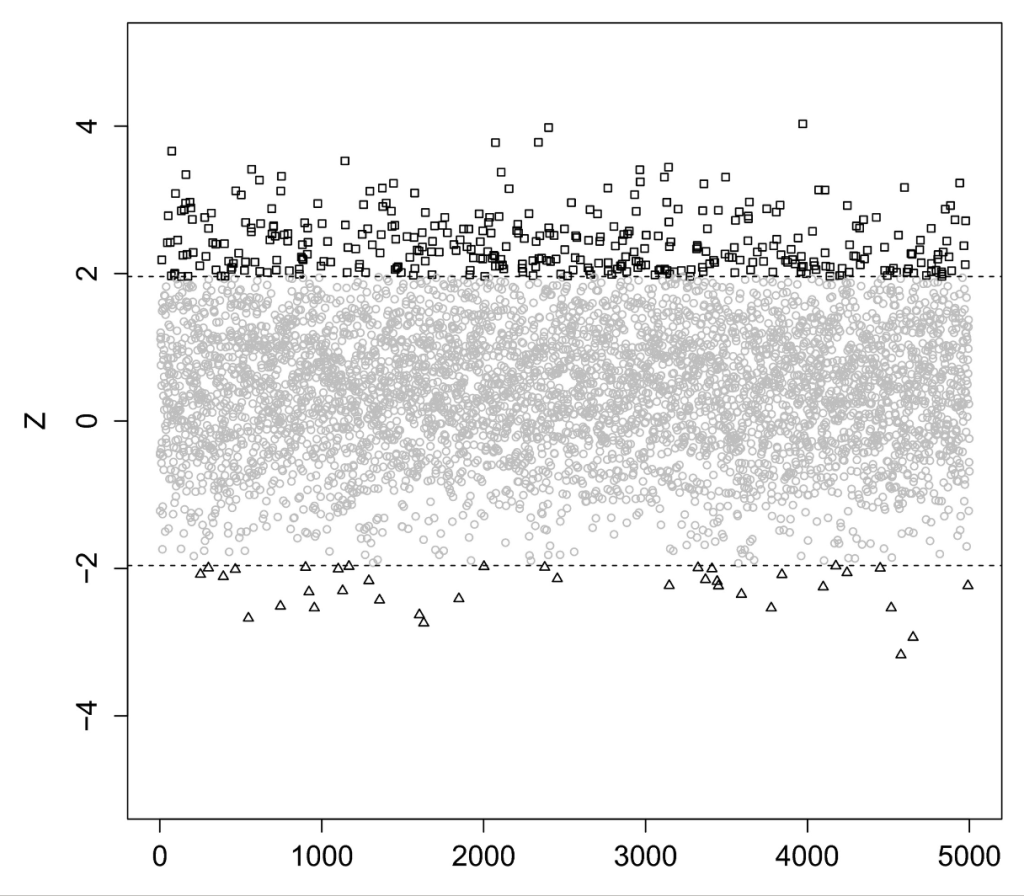
Gelman’s perspectives on significance align closely with Imbens’ views. Both statisticians emphasize the importance of point estimates and their variability over mere statistical significance. They argue that these values offer more utility for cost-benefit analyses, which often hold the most relevance in practical applications. Consequently, Type M (magnitude) and Type S (sign) errors are more informative than the traditional Type I and Type II errors, as they directly measure the accuracy of the point estimate.
Research has shown that “while that Type S errors are rare in practice as long as the analysis is conducted in a principled way, Type M errors are rather common” [6]. Type M errors are especially common in small sample sizes. Given that published research tends to favor significant results, many reported effects are overestimated. This overestimation can lead to misleading conclusions and a skewed understanding of true effect sizes in various fields of study. Another related issue is the limitations of p-values across different sample sizes. As previously mentioned, p-values become less informative with large sample sizes, yet they often lead to inflated effect sizes in small sample sizes. This suggests that p-values have inherent problems across all domains.
Over-reliance on and misinterpretations of p-values
Over-reliance on p-values has led to curious conclusions. In a study on drugs for atrial fibrillation, researchers concluded their results differed from previous studies because they weren’t statistically significant, despite finding identical drug efficacy [7]. This interpretation overlooks a crucial aspect: the primary concern regarding drug efficacy lies in the magnitude of its effect, not just statistical significance. In fact, the replication of the same effect size in the new study should be viewed positively, even if it didn’t reach the threshold for statistical significance.
Interestingly, in a study that tested psychology students, professors, lecturers, and teaching assistants on their statistics knowledge, none of the 45 students, only four of the 39 professors and lecturers (who did not teach statistics), and only six of the 30 professors and lecturers (who did teach statistics) got all of the answers correct [1]. This suggests that even experts make statistical errors.
Will the p-value for statistical significance be abandoned?
Although there are many people raising concerns about the p-value with its interpretation and viability, few are arguing that it is completely abandoned. Most research today still uses the NHST paradigm, making a complete shift away from it challenging. Additionally, p-values help in assessing the likelihood that observed results are due to chance, assuming the null hypothesis is true. This helps in filtering out genuinely spurious findings; Imbens acknowledges that statistical significance is still necessary for rejecting the null hypothesis [4]. None of the articles I read propose completely disregarding p-values, and instead suggest a more nuanced approach for interpreting them. While statistical significance might be less significant in the future, it will still play an important role in science.
References
[1] McShane BB, Gal D, Gelman A, Robert C, Tackett JL. Abandon statistical significance. The American Statistician. 2019 Mar 20;73(sup1):235–45. doi:10.1080/00031305.2018.1527253
[2] Estimating the reproducibility of psychological science. Science. 2015 Aug 28;349(6251). doi:10.1126/science.aac4716
[3] Abadie A. Statistical nonsignificance in empirical economics. American Economic Review: Insights. 2020 Jun 1;2(2):193–208. doi:10.1257/aeri.20190252
[4] Imbens GW. Statistical significance, p-values, and the reporting of uncertainty. Journal of Economic Perspectives. 2021 Aug 1;35(3):157–74. doi:10.1257/jep.35.3.157
[5] Gelman A, Tuerlinckx F. Type S error rates for classical and Bayesian single and multiple comparison procedures. Computational Statistics. 2000 Sept;15(3):373–90. doi:10.1007/s001800000040
[6] Lu J, Qiu Y, Deng A. A note on type S/M errors in hypothesis testing. British Journal of Mathematical and Statistical Psychology. 2018 Mar 23;72(1):1–17. doi:10.1111/bmsp.12132
[7] Chao T-F, Liu C-J, Chen S-J, Wang K-L, Lin Y-J, Chang S-L, et al. The association between the use of non-steroidal anti-inflammatory drugs and atrial fibrillation: A nationwide case–Control Study. International Journal of Cardiology. 2013 Sept;168(1):312–6. doi:10.1016/j.ijcard.2012.09.058